Knowing Thy Impact

Knowing Thy Impact
John Hattie's work on Visible Learning is applied to Mathematics in his book titled Visible Learning For Mathematics: What Works Best to Optimize Student Learning.  In this book, the authors examine the plethora of "research-based" instructional practices in an effort to provide recommendations for best-fit teaching.  In a seminar in Toronto this summer, John Hattie recommended that educators resist getting seduced into a single form of instruction and opt for an understanding of the impact of various types of instruction to produce significant results and maximize student achievement.  He labelled it the Goldie Locks approach to instruction:"Not too hard and not too boring". This reminds me of Vygotsky's Zone of Proximal Development.  Matching instructional practices and strategies with the student's readiness to learn.  In sum, Hattie et al.'s framework asks the teacher to consider when particular teaching strategies are most beneficial, and where a student is in his or her understanding of a concept.

Making Algebraic Thinking Visible

Making Algebraic Thinking Visible

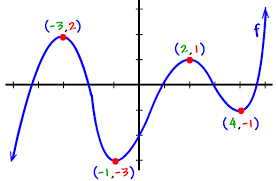
This clever problem would be an excellent way to lead student's into a dialogue about using different methods to solve a problem.  Further, it has an accessible entry where visually a student may be able to deduce the height of the table and it allows other student's to reason algebraically with multiple variables.  This could be used in an elementary class as an intro the algebraic inquiry, yet it could also be used as a "minds on" exploration in the senior grades before demonstrating how to solve equations with more than one variable.  Overall, it is a gripping challenge and would allow the students to engage in mathematical dialogic investigation.

Watch the video below by Presh Talwalker at Mind Your Decisions to see two methods to solve this problem.  It could also be solved using bar modelling from Singapore's Primary Mathematics program. 

Geometry Snacks

Geometry Snacks

I was intrigued by a geometry question I saw on  Twitter which credited authors, Ed Southwell and Vincent Pantaloni.  Geometry Snacks is a great mathematical puzzle book with many geometrical figures that will lead the student through several complex challenges.  The problems are fun, increase in complexity and allow students to see how many approaches one can use to solve a problem.  The first questions could be used to challenge elementary and middle school students, whereas the latter challenges involve the application of higher level mathematics and logic.  Once a student has solved the problem, the authors also provide further challenges. The rich geometric vocabulary makes this little pocket book, an excellent resource for teachers of Mathematics.


A Sample Question for Geometry Snacks as presented by blogger and author Presh Talwalker.

Sentences Stems

Sentence Stems - Helping Students to Participate in Academic Conversation

In our mathematics classrooms we want our students to have engaging conversations that encourage students to think critically about each other's ideas.  When students think critically they must challenge each other's responses and ask for clarification.  Being able to participate in scholarly conversation is a skill that needs to be taught; it's even more difficult for English Language Learners (ELLs) who are trying to learn the language and content at the same time.  This summer while taking my ELL Part 1 course I learned about the use of talk stems that provide students with sentence starters for initiating academic conversation.

A poster like this, hung on your classroom wall can be used as a form of reference for students when they are working in groups.  Making reference and modeling some of these sentence stems would be very beneficial in classroom discussion.

Poster taken from: https://mrlhuillier.wordpress.com/

Symbolab Friend of Foe?

Several of my students have been talking about the Symbolab website and Symbolab app for solving various math problems.  The site covers content in algebra, graphing functions, calculus, geometry, statistics, physics and chemistry.  Students can type in a problem or equation and pick from a list of solutions, complete with step by step instructions and explanations.  It is certainly a helpful tool when struggling to complete homework, but will students use it properly or simply right down solutions? After trying the Symbolab website for myself I have to say I'm impressed with some of its capabilities, however, I'm a little reluctant to recommend it to students because of the ads that keep popping up for dating sites.  Here is a screenshot of the solution provided to me when I typed  2x-y=8  and 3x+y=12 into the search bar. 

What do you think?

"New Math" vs "Old Math": Tips for First Year Math Teachers?

Being a young, new teacher fresh out of Teacher's College is frightening! Now with the program being 2 years, it still seems like what you learn in practicum as a student teacher is not nearly enough and there is so much more to learn! And with this, so many things have changed since we were students - the internet has changed the way things are being taught from traditional math on a chalk board to interactive, online approaches, videos, and more! The learning curb is steep and even if an LTA presents itself, there's only so much time for us to prepare for it and then so much more learning comes with it.

Being a science teacher, I have never taught math (hence taking an ABQ). What is your advice for new math teachers? What are the best approaches? What are the must-do's vs. the things that might not need to be emphasized as much? I found a thought provoking article called Meet the New Math, Unlike the Old Math that encourages a new approach to math (written in the US). Away from teaching how to solve equations but more on how to analyze functions, as well as shifting more towards big ideas in the curriculum and having more communication about mathematics. The article is a bit long but quite an interesting read. Is this the approach that most math teachers frequent now? Or is the emphasis focusing on teaching concepts one by one from the curriculum? What are the best strategies to making math education fun and effective for all (student and teacher)?

Math Prodigy - Thoughts??

Math Prodigy website link

Although not as common in high school, I have heard the game 'Math Prodigy' thrown around a lot by students and teachers! I myself have had no experience with the game (I just created an account out of curiosity today) but it has me thinking if it could be an effective tool for 'gap filling' for Intermediate (Applied/LD classes) as well as math tutoring outside the classroom, such as fun homework practice since it is linked with Ontario math curriculum from Grade 1-8. Has anyone had any experience with Math Prodigy and could share some thoughts?

What I liked about the video on the Prodigy home page is that like many other online websites, Prodigy allows you as the teacher to monitor student progress to see how well students are grasping concepts broken down by topic. It also allows you to create your own assignments for students which is a neat feature I never knew about! There are also virtual manipulatives and you can choose to use Ontario math curriculum or Prodigy math curriculum (whatever that may be). Lastly, it's so multifaceted - from being able to see feedback from students, use it as formative assessment and a neat differentiation tool. Plus... it's a game! I'm assuming that's part of the reason why student's get hooked on it. Would love to hear what you think about it since it seems like it would be a worthy tool, but would like to hear any first hand experiences with it first. Thanks!

Math is for everyone!

                               

Math is for Everyone!

                                       

I saw this cartoon and thought of my students in my math class. The students in my class are always complaining that math is the hardest subject and you have to have a mathematical mind to even do the questions in the course. So I asked them why they feel like it is so difficult and there simple explanation was "it's never the same sir! There are so many question to know." Then it hit me they were trying to memorize what to do without fully understanding the why, we do what we are doing and fully understanding the concept that was being taught. So from that point on I started to focus on the why, not skipping any simple steps in solving for equations.  Getting my students to develop steps for understanding how to go about solving anything from a linear system to a word problem within the course.  I wanted them to learn to think about what they learned and apply the knowledge that they got in class.  I wanted them to know anyone could do math if they work hard and tried their best. I didn't want them to think that it was a clever scheme meant to trick them. So after I was done my lessons I would give the students a question based on that days class and have them answer it. I would not just have them calculate the question but I had them write out the steps they took in words to solve it.  Then I had them get into groups of two and all they could do was read the steps to the other person to see if that other person understood what they did. This forced them to think about what they were doing rather then just doing it. When they were in those small groups they really had to communicate their thought process to each other.  I repeated this with my class for a week. At the end of the week I found that they were understanding the why better then they did at the beginning of the week. Has anyone else ever tried a similar method?  How well did it work for you?

Frustration in Math

In math, I feel like everyone was has been so overwhelmed where there is a mix of frustration, anger, confusion, sadness and disappointment during the learning or practice of a math concept.  Now as a future teacher and a current tutor, I can see it in my students' faces sometimes and it is hard being on the other side of the knowledge.



I saw this quote the other month on Twitter and it made me smile.  I feel like in school, math is looked upon more of a nerdy thing and "not cool".  Because of this, I feel like it adds to the overwhelming emotions at a tough point in math.  I feel like in sports, it is more known in social media that struggling is part of the grind and you will get better because of this.  It is funny how this does not translate to the struggle in math (or any other subjects).

This brings me back to the quote I saw above.  I think that math is very cool, is needed in many facets in life and is fun.  I feel like the discomfort can push students away but if they are shown this quote, know the importance of math and that they understand real life applications of math, they will be more positive towards the struggle. This could definitely benefit students and although is not as easy as what I wrote above, I believe that it is a strategy worth exploring.

I know it will be a future poster in my class.

Any thoughts on this?

Maksym Cord

The Amazingness of Calculus

This is a PSA,

I think that calculus should get much more credit on being a really cool course.  Maybe my teachers did try to tell us this, maybe not but I think something more should be done to show this.

When learning about calculus through a book, it blew my mind.  This was especially so because I was adept at advanced functions and learned to work with linear equations and figuring them out and how to use them in real life applications.

So I was reviewing the book and it soon told me that linear functions used methods to find out information on straight lines.  That's awesome you say but wait theres more!  Then it went on to say that straight line relationships are quite unrealistic in life and that in real life, the lines are more curved (like the one below).




So what?  Well what blew my mind is that somehow, people figured out how to solve for information on curved graphs to then solve for real life situations.  Further, the creativity needed to understand that as you zoom in enough on these curved lines, they will end up as straight lines which will then let you solve like a linear equation.  They then figured out methods to get the sum of these calculations to use to then solve a whole curved line. WOW!

Maybe I should get more hobbies but people need to see this!

I hope to plan out a way to communicate my enthusiasm as a senior math teacher.

Maksym Cord

The Harder he Material, The Better I Do?

Hey all,



I wanted to tell you about my experience with senior math courses throughout high school.

I remember before I would change schools (elementary to middle, middle to high, high to university), teachers would make a point to try and get you line by saying that "oh the teacher won't chase after you for marks and they will just fail you."  To me that worried me but I soon found out that teachers definitely do chase you for marks (whether elementary, middle or high school) (though not as much).  This sort of gave me a relaxed outlook on really trying in school.

In grade 11 I heard this speech again but for some reason, I really believed it this time.  I believe this was due to my parent and family telling me the same sort of thing.  When this happened, I started really focusing and trying in school.  At the same time, I entered into "Advanced Functions" which was notorious in the school for being hard.  For whatever reason the mix of effects from these two things made me really try especially hard in math class.  I think that the complicated looking symbols and equations helped this aswell.

I begun really paying attention and doing my homework everyday.  This brought my typical 70-75% average every year in math to the highest in the class at 96%.  This showed me how powerful homework and paying attention was and I learned through this that math was fun and was just basically puzzles.

This then lead me to enjoy the math and made me want to teach others how fun it could be.  This then lead me to here, aiming to become a high school math teacher.

I hope I am able to instill this outlook for my future students.

Thanks for reading, does anyone have any ideas on how to do this?


Maksym Cord

Why do I need to learn math?

Why do I Need To Learn 

Math?

                         

I have been a secondary school teacher, teaching for eighteen years, I recently started teaching math and have fully learned to appreciate it as well as learned to enjoy it!  

My students always ask the same question  "Sir why do we need to do this? Or what is the point of even learning math?" Just to let you know its more then telling them there will be a test on it in the future. So when I begin teaching a math course I always show this YouTube video I found that explains why in fact you should be learning math. It show students that math is everywhere and that taking math opens a lot of doors in the future for careers.  It also tells them that math is for everyone if you hang in there the reward of solving a problem and understanding is amazing.  

I know as math teachers we need to teach curriculum but I think it is important to inspire our students to let them know why they are learning it. To motivate them to want to learn, to love learning.  To let them know it is a challenge and that we grow from making mistakes and learn from them! 

Let them see you love what you do, share your passion! 

This video is great for any high school math class as an introduction to your course. Here is the link to the video I was talking about:

https://youtu.be/90wFGf534ao

Using Math Talks to Improve Metacognition and Communication in the Math Classroom

This will be an anecdotal post about how using regular math talks in the classroom boosted the confidence and achievement of even the most math averse students in my grade 7 homeroom.


The year was 2015, I was hired for my first contract position in a Grade 7 homeroom. I was ready to make my mark on the education community and get involved in every aspect of the school community I could and become the BEST TEACHER EVER. Well, I succeeded in being the best teacher ever - I have the award covered in minion stickers that I received from a student for the end of the year - but I also enrolled in an intense course of Math PD.

The math PD that was all the rage that year was focused on Math Talks. Normally, I am a little hesitant to go to PD because sometimes I have found it sounds really nice but is a logistical nightmare to try and incorporate into the classroom. Not this time...

This time we were lucky to receive a book called Making Number Talks Matter - Cathy Humphreys and Ruth Parker. This book quickly became my "go-to" book when planning math lessons (along with my Van De Walle). In this book you will find instructions on how to do math talks and what they are all about.

I will summarize here:

A math talk is a 10 to 15 minute talk that only requires posting a pre-selected question (you can use examples from the book and then adapt your own) on the board and asking students to solve it.
The catch - they can't use a calculator or pencil or paper. The math has to be done entirely using mental math strategies.

Here is a problem - try and solve it in your head and don't scroll down. Think of what strategies you used. (*hint* All questions are written horizontally to avoid rote algorithms like "Stack and solve")

    

9 x 16

But who cares about mental math? (We all carry calculators in our pockets now anyway.) Mental math in this case is not about knowing your times tables or being able to solve problems quickly. Here it is about selecting the appropriate strategy and breaking down a question into parts. 
When students are ready to answer they give you hand signals (shown below). The teacher then asks the student to provide their answer, and asks the class if anyone had a different answer. Once everyone has agreed on the same answer, the teacher scribes what the students suggest for their strategies. As a teacher you would ask for several strategies and I like to name it with the student's name.

Which strategy did you use?

So my anecdote goes like this. I used this everyday for about 3 months, and I gradually saw the students become more and more confident solving problems. One day, near the 2 month mark, one of my weakest math students (who NEVER participated in math talks) shyly raised his hand. He had an answer that was already on the board and now he was confident his technique worked. He shared his thinking and we wrote out his strategy on chart paper - we named it "James's Strategy" and kept it posted for the rest of the class and next... The next day as we were doing a math talk, one of my students answered a similar question to the day before . When asked what strategy they used, they replied "James's Strategy" - my shy James beamed :) It was such a proud moment for him to be able to contribute to the classroom. 

From that moment, this student began participating regularly and raised his mark from the low 50s into the high 60s. For me it was a very proud teaching moment and I can never say enough good things about number talks. 

Go and get yourself a copy now! 

ABQ Math Blog: Bundled Courses: The Art of Math

ABQ Math Blog: Bundled Courses: The Art of Math: This year, the coolest combination of subjects fell into my lap. I had a short term LTO in this bundle course called the Art of Math. Yes,...



Great article, I also really agree with what you have shown.  Art can play a huge role in learning math.  This also comes at a great time seeing that art is being brought into the STEM courses for its applicability and researched benefits.  It only makes sense as it provides a visual learning style and therefore will help visual learners and give non-visual learners another way to think of the concepts.  Lastly, it is shown to create deeper understanding of math (TSF ,2018).



I wonder if incorporating math with phys. ed, would provide great benefits?



References

Teacher Support Force.  (2018).  Teaching Math With Art.  Retrieved from http://www.teacher-support-force.com/teaching-math-with-art.html

Bundled Courses: The Art of Math

This year, the coolest combination of subjects fell into my lap. I had a short term LTO in this bundle course called the Art of Math.

Yes, I couldn't believe it either -- two of my favourite subjects in one perfectly bundled course!

If you were thinking, how does that work? Let me introduce you to my amazing colleagues:

@briscoeclass & @mrsvankesteren on Twitter.

These ladies have been incredible innovators changing the way math and art are delivered. I encourage you to watch this video as they discuss their journey to bundling these two distinct concepts into a whole-brain focused course filled with engagement and understanding.

My experience in this classroom is what sparked my interest in getting my Math Qualifications for grades 9 and 10. In this class the students worked on math concepts with the math expert and art concepts with the art expert... but then would apply them into projects designed to highlight both concepts at once.

During my short time in this classroom, the students were looking at parallel lines and traversals, and how certain rules would help you discover the measurements of other angles... They would then connect these concepts to solve for interior angles within an image:

This is just one small example of how the two subjects could be blended together. The course was based on experiential learning and application of math and art principles.

If you watched the video you know there was a positive effect on student learning. Students were so engaged and learned so effortlessly they felt as if they had not actually had to learn it... they just knew it.

What other blended subjects do you think could work well together in a course bundle?

Oral Exams in the Math Classroom

During my last semester of teachers college, I had a professor mention that he always tries to incorporate an oral section into his written tests in the math classroom. He would bring students up one by one, and have them complete one section of the test verbally. At first I thought this idea was crazy, but the more I thought about it I realized that a lot of students would actually really benefit from this in the math classroom. I cannot remember a time in any of my high school or university math classes where we had to orally present our findings or understandings. However, I was not complaining because I tend to do better when I write my answers down rather than vocalizing them. Nonetheless, this is not the case for all learners and some students would do much better explaining their answer and thought process out loud rather than writing it down. This puts these types of learners at a huge disadvantage in the math classroom and may even discourage them from continuing to take Mathematics in the future since other classes such as English or French may better appeal to their learning style. Throughout my tutoring experiences I have seen this first hand. When I first started tutoring one of my clients, I was not quite sure what to do because at the end of the tutoring session she seemed very prepared for the test, however she never ended up doing as well as I thought she could do. During the session I would quiz her on the content and ask her to verbally describe the steps she would take and she would be able to communicate this perfectly. However, she would then tell me that she was not quite sure how to put this down into words on the test. Maybe there are other students out there that would benefit from taking an oral rather than written test? How will we know if we don’t try! Plus, you’ll be helping your students develop their communication skills, which will be setting them up for success in their post-secondary lives.

What do you think, would you incorporate an oral exam into the math classroom? What are some pros and cons of using an assessment such as this?

What is so hard about word problems??

Have any of you ever thought about why some students struggle so much with word problems? Although I have not had any experiences teaching in the math classroom, every time I started tutoring a new student one of the first thing they said was "I can't do word problems". They can know the math inside and out, but the second they see math in the form of a word problem or real-life application, they suddenly don't know what to do. Have you ever thought about why this might be the case? 

As I was thinking about this on my way home one day I realized that maybe part of this is because we as teachers assume that students already know how to solve problems, even though this might not always be the case! From that moment on, I decided that once I become a math teacher, one of the first lessons that I will incorporate into my math classroom is taking the time to teach students how to approach word problems and how to develop their problem solving skills.  Developing good problem solving skills in our students will benefit them in all aspects of their lives, not only mathematics. By giving students an outline of the steps they can take to solve a problem, as well as giving them time to practice this process, you are truly setting them up for success in their future. Unfortunately, some teachers may assume that students already have a good understanding of this process (even if they do not) and may not teach students this important life skill. For example, when I first started tutoring a client in grade 9 math one of the first things she told me was that she was extremely uncomfortable with word problems. Anytime a word problem came up, she would be very overwhelmed because she could not figure out how to approach the problem. The first time this happened I was not really sure what I could do to explain the problem to her. I quickly realized that this problem had nothing to do with her mathematical ability, but instead with how she tried to approach the problem. Therefore, I had to take the time to walk her through each step of the problem solving process. The first step was what she really struggled with so we spent a lot of time practicing how to analyze word problems to decide what information is important, and what information is not important. Then I would have her write out this important information, draw a picture if possible, and write out any mathematical formulas she thought she might need. At first she needed a lot of assistance throughout this process, however as time went on she needed less and less help. Over time, she became much more comfortable with word problems and can now apply these problem-solving steps without even being told. All she needed was someone to take the time to explain to her how to approach a problem. 

What do you think? Is this something that you think you might incorporate into your classroom?

So I am Nervous About Teaching Math, Please Help!

So if you know math these days, you almost certainly know Khan Academy (https://www.khanacademy.org/).



I am sure the usual reason people end up there is because you are a student and you have a math test tomorrow.

"How do you know!?" you may ask, "Your not a scientist!" you say.

"You're right." I say while crossing my arms, a smile growing on my face.



Well that situation was me in high school/university though I was more of an early bird when it came to studying for my test.  So although my test was not "tomorrow", I still needed a new way of learning a math concept that my teacher was not providing me.  His was of explaining it while showing it through the video and my option to replay it many times was a life saver.  It helped me do well on many tests.

More recently, for my intermediate math ABQ I was tasked with doing a bunch of practice sessions for 15 different lessons where I had to solve 5 questions in a row with no mistakes, for each lesson!  So, I have been finishing up teachers college and away from my math books for a little and man have I forgotten a lot of things that students go through in math, it was such a throwback seeing all of these questions I used to do.  Some of them I forgot how to solve and I was worried I wouldn't be able to get a perfect score on these questions.

Enter Khan.  After each mistake a video suggestion would pop up asking if I wanted to watch it to help solve the question.  So I did and the videos were always spot on.  They reminded and taught my exactly what I needed to know.  They made math fun.

I think this is such a great resource for teachers, learners, parents or anyone interested in math!

What're your experiences with Khan Academy?

Thank Khan,

Maksym Cord

Teaching Math should shift toward new methods

Teaching Math should shift toward new methods!

    We've been all taught math through classical ways. First, the rule will be provided to you and then questions bearing in mind that practice makes perfect. It is necessary to have a deep understanding on how to use those rules and formulas in real life and how to make use of them. Here are two ways in order to improve the math taught at the present time.

Math of the present time!

  One way is by having specialty teachers assigned to teach the subject.Teaching Math for younger students from a homeroom teacher (with no Math background) could have a negative impact about how interesting or boring the subject can be. A specialty teacher can relate a lot to real life example while teaching Mathematics. That makes the lesson more interesting and appealing to the students. Moreover, a specialty teacher have multiple ways to explain the concepts when the students find the book confusing or the way taught is difficult to understand. A specialty teacher can manipulate any formula and makes it easier to grasp. In addition, a math specialty teacher can always relate to old concepts being used so that way students can have deeper understanding.

   Another way is to get students engaged into application of mathematics. For instance, the use of iPad/Tablets and more technological tools that can enhance to a great deal student’s learning. It is important to have knowledge about the basic rules but sometimes it gets overwhelming that students' focus will be more toward scoring higher in the exams and therefore their creativity is killed. For instance, provide all the rules and formulas to students and make them synthesize a solution instead of memorizing. Doing so can enhance students learning by engineering creative ways to get to the solutions. Having done with the task, then provide an application where the solution synthesized can be used. Therefore students will never forget about the concept and math would be fun to understand.

Math of the near future?

   Finally the big question to ask is when such a shift take place? And if it happened, would it be beneficial to the students?

Why Math is a universal language?

   Each one of us was born in a certain place at a certain time. None of us has a chance to decide his/her race, gender, nationality and native language. As we grow older, we start to assemble the puzzle in order to arrive to a theory that specify the meaning of our existence. We go to school and we start first by learning the alphabets, then words and sentences until we're able to make paragraphs and essays and later on write articles and books. It is a gradual improvement on how communication became easier through learning a language. Eventually, everything starts to make sense. 

Similarly, Mathematics is based on common sense. At a younger age someone would be able to count and to differentiate what is more or less. Also, kids learn from how much they possess and how much more they have than others etc... students at school learn numbers from tiles and therefore they start to put the puzzle altogether as they grow older. We use math in our daily life despite your occupation ( teacher, doctor, engineer, carpenter, lawyer etc...) . When it comes to sciences, it won't make sense without the use of mathematics. For instance, in physics math is needed to perform all the calculations needed algebraically. In chemistry, math is needed to do all stoichiometric problems as well as the graphs associated with physical chemistry. In  Biology , math is essential for finding probabilities and distributions of datas. In economics, math is essential for graphs and for the different calculations associated and the list goes on. Therefore, in order to communicate science someone needs to speak the universal language which is mathematics. 

Mathematics is always associated with solving problems. Yes, it is widely used to solve problems given by a teacher if you are a student. At the end, regardless of your occupation you will arrive to a solution. First, you have communicated the problem and then you have used your acquired knowledge about the subject to engineer a solution. Scientists from all over the world gather at the CERN ( European council for Nuclear Research) in Switzerland and in NASA in order to understand the universe better and make a difference in our life. Those scientists rely on mathematics as their universal language in order to communicate better their ideas. In addition, since mathematics is a universal language and it helps narrow down the differences between cultures, why not using it to "solve problems" between countries? 

So I am Nervous About Teaching Math, Please Help!

So here I am.

I am in an intermediate math course aiming to teaching high school level math.  As mentioned in my last post I am going to my senior level math after this.  I am very nervous.

"Why?!" you may ask.  Well, I haven't taught high school level students.

See, I did my teachers college degree in primary/junior.  This means that all my teaching experience was in those ages.  I did do an alternative practicum (practicum with no teaching) at a high school but I did not get any teaching experience.

So here is the issue: I am nervous about teaching high school students and I am nervous about not finding enough resources to teach math!




Firstly, I feel like teaching younger students is easier in the way that they are young that I don't get nervous speaking in front of them.  High school students on the other hand are older and I am worried that they can more maturely judge my lessons (like an associate teacher)...I mean I have heard that they don't and I am overthinking this but, is that the case?

Secondly, I have done all my teaching in primary/junior levels as mentioned before.

So I think I will just have to teach in front of high school students to get over that but, with the resource thing I have a plan!!!!

I created a Google Docs link:https://docs.google.com/document/d/1LS07NLGjWD8gDHDK_fppd-4Bth0lbeUFSZnGHo42PEQ/edit?usp=sharing

Please help my journey and add some good resources/websites you have!  Feel free to watch it aswell to get some new ideas for you.

Thanks,

Maksym Cord

Why I want to teach math

I have been an educator for four years now and have been lucky enough to have packed in a tonne of experience in that amount of time. I recently switched panels from Elementary to Secondary; my teaching record consists of 4 different elementary schools and 2 highschools. For all you mathies out there, that is 6 different schools.

In my Elementary days, I was lucky enough to teach in a grade 7 homeroom consistently. I have always loved math, (Aside: my teachables are Art and French), to me it was like another language that the whole world understood. I loved the logic of it and the straightforwardness, right or wrong, you followed the steps, or you didn't. 

However, now, as an educator I see that Math isn't just black and white. It is still a language to be learned and used, but it is not simply about getting the right answer. Math is much more about the thinking the reasoning, the rationale behind each move. Often, I feel like solving a math problem is like tackling a puzzle (And who doesn't love a good Sudoku).

Anyway, I had never intended on teaching math, being inclined towards the arts as I went off to university. Recently, I found myself falling back in love with it when I had to teach my grade 7s. It became my favourite subject to teach and I would pour my creativity into coming up with ways to get my students involved. 

Moving to secondary, I have now been out of the math room for nearly a year (save for when I get the chance to supply in a math room!). I had an eye opening experience when I had the opportunity to do a short LTO in an Art of Math Classroom (post on that to come later); it was a whole new way to look at things.

I believe that the future of education will move towards blending subjects and focusing on how the big ideas in various curricula overlap and I cannot wait to be a part of it!

Why I Want to Teach Math

Hi there,

Growing up, I didn't love math and I didn't dislike it.  It was just "meh".  I did decently well, probably averaging a B-.  Going through school, when you graduate and moved from elementary to middle and middle to high, the teachers always said "oh teachers won't care if you don't understand, you'll just fail" or something of the sort.  This motivated me to start putting work into my school.

In grade 9 and 10 I did around a 75% and then at the end of grade 10 I got the "scare you" tactic again about the senior level math courses.  Now I was worried, so I decided the next year to take math seriously which, meant doing my homework.

At the same time, I got a new teacher named Mr. H, he was a funny, nice and relaxed teacher and made the idea of math much less serious in my mind.  He always gave us homework and time to do it at the end of the class.  It was this homework time and my time doing homework after school that bumped my average to the highest in the class at 95%.  I then started slacking on my homework and dropped all the way to a 75% again.

So what's the point of this?  Well, I am glad you asked cause it was during this time where I realized that if I practiced something I knew I could do well in it.  I also realized that math was fun and it was basically like solving puzzles.

This stuck with me and in teachers college, became my favourite thing to teach to my primary and junior students.  I realized that I want to teach intermediate and senior grades for the maturity level and the math done in those grades.

So here I am.  I am doing my intermediate math and upon completion will do my senior math next semester.



What was your journey to teach math?

Maksym Cord