Helping a friend with Math

Today as I sat for my pedicure (forgive me, I was supposed to be doing my homework! Report cards are due soon) my manicurist's son was upset. His mother thought that math was just facts and that to do "math homework" it should be worksheets with drill and kill questions. Martin tried to explain to his mom that math was much more than that. (He is in grade 5). He explained to her that the thinking games on a math site that look like computer games, is in fact practicing math. I pulled out my iPad and had him work on the app Dragon Box (ok, I've said it before, I love this game!)When I told Martin to play it, He was adament that it was NOT a video game (as he was grounded)! She agreed when I explained the algebraic connection of isolating the variable -- the box alone on one side and he played and got to the third chapter before I was finished! I told her that I would help her explore more math and science "games" on the web for the summer! Does anyone have any other suggestions? Thanks!

Math and Music

After reading some of these blogs, I like the idea of connecting math to the arts. Let's be honest, math is not everyone's favourite subject! As a teacher, being able to connect math to different subjects is key for students (for whom math is not their favourite subject) in order to relate to the math world and understand why we need math.

For myself, this was not always an easy task. This website is great for connecting math beyond school.

http://mathcentral.uregina.ca/beyond/articles/Music/music1.html

This link will take you to the part of the site that specifically connects math to music (something that I find is not done that often). It connects music to things like fractions (a more obvious connection) and the Fibonacci sequence ( a less obvious one).

You can search in the "math beyond school" section anything that would like to relate math to. This would be a good activity to do with students during class time OR integrate this website into a project.

Enjoy!

How to Marry the Right Girl: A Mathematical Solution

I found this when looking through a website; the title seems humourous, but it actually explores the method of optimal stopping, or considering the "Secretary Problem".  When faced with many choices, a person should go through the first 36.8% of their sample, and not choose anyone in that first batch.  After the first 36.8%, you should stop at the one that you like.  Either offer the job (or propose or whatever) to the first one that you are satisfied with and forget the rest.  This is more strategic and likely to bring about happiness more than random chance, thus, mathematically makes sense.

The problem is explained in a book by Alex Bellos, The Grapes of Math, and discusses Johannes Kepler's problem in finding a wife.
Short but interesting read.  Something that might be a good high interest activity in a math class; read the article, and have students make up their own "Secretary Problem".

Link to article:
http://www.npr.org/blogs/krulwich/2014/05/15/312537965/how-to-marry-the-right-girl-a-mathematical-solution

What do Survivor, An Executive Superintendant, and the Mathematical Processes Have in Common?

There is more than one way. As I was watching Survivor with mom last week, which is her favourite show, I made a connection with math in the way that the contestants were going about the challenge to win immunity. If you have the time to watch the challenge, you will see what I mean.

At about the 1:50 mark, the commentator notes how Spencer is "struggling" and Tony is off to a fast start. Tony it should be noted, uses more of a trial and error method using his athleticism and speed, while Spencer does everything more methodically, trying to think his way through each part of the challenge without making a mistake. And at 4:30, the commentator again notes just how far ahead Tony is.  As much as I want to tell you about how it ends, I'm going to leave you in suspense hoping that you'll watch the video!

The point is that even though these two particular contestants used very different strategies, both strategies worked better than the other at different points.  It should also be noted that if Spencer used Tony's method and vice versa, each might have struggled rather than have any success at all.  What does this have to do with an executive superintendant and the mathematical processes?

In a May 16, 2014 CBC article, Hamilton-Wentworth District School Board executive superintendant Manny Figueiredo said, "We need to understand that there's more than one way to teach math. Some students might learn using concepts like borrowing and carrying over, while some might learn better using pictures and language."

If we take Figeiredo's quote and what we see in the Survivor video, and connect it to the mathematical processes, I think we should get a good idea about how we need to be teaching math. Here are some selected quotes from the curriculum:

"Teachers...  help students to develop and extend a repertoire of strategies... when solving various kinds of problems."

"Good problem solvers...  recognize when the technique they are using is not fruitful, and to make a conscious decision to switch to a different strategy, rethink the problem."

"Students need to develop the ability to select the appropriate electronic tools...and computational strategies to perform particular mathematical tasks."


 "Developing the ability to perform mental computation and to estimate is consequently an important aspect of student learning in mathematics."

It really isn't enough to simply teach the equation of a line, how to find the middle of a line segment, or how to solve for a variable.  According to Survivor, Figueiredo, and the curriculum, we should be taking a wholistic approach.  We shouldn't just do this to reach more learners, but also to teach our students to think on their feet and adapt to the situation. That would be to create a critical thinker. Do you think that if Tony or Spencer had changed their approach at some point that the race might not have been as close as it was? It's food for thought.

Constructive Feedback

             In math, I think it is common, when marking, to have the attitude "its right or its wrong". Consequently, this results in either a check mark or and "x". It is important for teachers be constructive with their feedback. What has been done well? What needs some work? What are the next steps the student needs to take? I first saw the following exercise during my undergraduate degree in a course called "Mentorship and Learning". I have also used it with my own students during placement to help them to understand the importance of constructive feedback during peer assessment. It is not enough to say: "good job! awesome!". We need to be specific in our language. I hope you will find the following exercise as helpful as I found it.

             During this exercise you select 4 volunteers and have them leave the room. With the remainder of the class you give one person a tennis ball and have them put it in their desk. Each of the volunteers will come back into the room one at a time and be told to ask 3 people of their choice 3 yes or no questions to help them find who has the tennis ball. Before each volunteer comes in, the class is given instructions on how to answer the question. In between each question the volunteers will be told to move on to the next question quickly.

             The first volunteer comes in and asks their questions. The class remains silent and does not answer any of the questions.

             The second volunteer comes in and asks their questions. The class responds positively, but is not helpful. For example: Question: Is the person who has the tennis ball female? Answer: Thats a great question!! Question: Does the person who has the tennis ball have brown hair? Answer: I like the way you worded that!

             The third volunteer comes in and asks their questions. The class responds negatively. For example: Question: Is the person who has the tennis ball male? Answer: That is not a good question! Question: Does the person who has the tennis ball have brown hair? Answer: Why would you ask that?

             The fourth volunteer comes in and asks their questions. The class responds positive and CONSTRUCTIVELY by helping to lead them to the next question so they can find the tennis ball. For example: Question: Is the person who has the tennis ball female? Answer: Yes. That is a really good question. Her hair is very long. You should ask what colour is it. Question: Does she have brown hair? Answer: No she has blond hair and she is wearing a t-shirt.

             By the end of the exercise, the fourth volunteer will be the closest to finding the tennis ball. Each volunteer is given the opportunity to share their feelings about the feedback they received and if it was helpful. The teacher then compares the first volunteer to receiving feedback that consists of check marks and x's. This lets the student know whether they were correct or incorrect, but gives them no information on how to improve. The second volunteer is compared to positive feedback that doesn’t give students a next step. There is always room for improvement and it is important for students to know what they can do to improve their work (being more specific, organizing their work more neatly, including a "therefore" statement, showing all of their work, etc.). The third volunteer is compared to negative feedback where students are only informed that they were incorrect and not given any feedback on what they could do to improve, where they went wrong, etc. The fourth volunteer is compared to constructive feedback where students are given specific details for what their strengths were, what they need to improve on and how. 

             This exercise is very effective in illustrating the importance of constructive feedback for both teachers and students. This is something that would be great for a professional development workshop, as well as for a classroom before student are going to go through peer review, a gallery walk, or some type of peer assessment. I think that it is also beneficial in providing students with ideas for what questions they can ask after receiving feedback. What should I have done differently? How can I improve? Where did I go wrong?

Flipped Classroom in a Math Class

When I came home from school Friday afternoon, my new copy of Professionally Speaking was waiting for me. At our house this can be confusing because my daughter is also a teacher and her copy was there too! When I read the cover, as I was taking it upstairs to get ready for a night of Report Card writing, an article caught my attention. "On the Flip Side" by John Hoffman was about a topic that we talked about in my 7/8 Math course this year. When I first heard about flipped classrooms, I thought what was different from when I went to school and we were required to do a reading about a subject to be prepared to talk about it the next day. ("READ CHAPTER 7 for tomorrow-- there may be a quiz" was the battle cry of my youth.) Today, instead of assigning chapters or concepts to read about, students are required to watch short videos about a lesson (or the entire lesson) and work on applying the learning in the class the next day with the teacher. This concept would hold the students accountable for their own learning. It also states that it is more work for the student but is it? The student is still required to listen to mini-lessons. The student is still required to do practice work on the concept taught. The student is still able to ask questions and receive clarification and descriptive feedback in a timely (and some say more) timely fashion. The student is required to take quizzes and other assessment pieces. To me this holds the student accountable with the same amount of work! How can I incorporate this in my math teaching? I can go back and assign students to create minds on activities about concepts that are going to be taught. I can then tape the students teaching this for the class and have them downloaded to a private youtube channel where students will be responsible for watching and responding to their classmates. This could be the start of something that can be expanded on as we see the benefits of such activities.

JUMP Math

This program is currently being used in Canada for classes 1-8 and uses a balanced approach called “guided discovery”.  Essentially, students explore on their own (with guidance), and go through a series of challenges increasing in difficulty, receiving immediate feedback.  This program allows students to work at their own pace and breaks down lessons into manageable chunks.  This helps everyone learn better, because they move at the speed they feel comfortable and never get overwhelmed with information.  This means LD kids can learn the material just as well as academic students.  Each small concept is immediately practiced and assessed.  This keeps students more engaged.  By learning a small concept, immediately practicing it, then immediately getting feedback, it resembles more of a video game format of a reward system – immediate feedback for accomplishing a task.  Even students with short attention spans can get through the challenges and learn effectively.  In addition, this format of learning ensures that no child gets left behind and greatly reduces the chances of students developing gaps.  Kids get a more solid foundation on which to build in the future.  The JUMP program also provides training and resources for teachers to make implementing the program easier.  For more information, visit jumpmath.org.

Seven Mathematical Processes

If you are like me, you may have been graduated from the Faculty of Ed for some time now.  Maybe not.  But if you aren't familiar with the seven Mathematical processes that are just as essential as the curriculum, then you should definitely read about them in the curriculum documents.  Not comfortable with the concepts?  Need more?  Don't really understand what it all means because you are someone who needs to practice or be shown examples?  

Then check this out: 
http://www.learner.org/courses/teachingmath/grades9_12/index.html

This link will take you to the above PD session for the processes.  Be critical, though, it is an American site, and it is missing the processes of "Reflecting" and "Selecting Tools and Computational Strategies".  

Happy learning!

Math and Art

How many students do you think relate math and art?  Many students who tell me they don't care for math tell me that they are more creative and don't think so logically - how about you?  Well, when I saw this article I thought it was fantastic, as it is all about how math inspires art!  In the Discover magazine, they share math inspired works of art, relating to equations and geometry.  http://discovermagazine.com/2014/april/11-visions-of-math 

Take a look at these examples of art that are a result of math!

What a great way to integrate math into art class, to help recognize its far-reaching boundaries and appreciate its creativity!  Enjoy the other artwork in the article.

Osmo

I saw this article today and thought I would share it with you here.  Osmo is an interactive iPad accessory that according to the website "brings real-world gameplay to the tablet."
I particularly loved the tangram activity that was shown on here - could be a great tool in the math classroom.  I have attached a video  below.  I would love to see what other math games/puzzles could be created.

math gaps

Seeing as how today's topic was about the gaps we are experiencing in our math adventures I thought I would share one I experienced today. I tutored a grade 10 student in the grade 10 applied math course (the first time I have tutored in over 2 years) and found the experience eye opening. I had heard from the teacher that she required a lot of help but I had assumed that it was in the concepts they were learning in class. We started with factoring and after explaining and going through some examples in the book she told me she was confident to do some on her own so I thought great, lets give it a go (albeit a bit naïve). The student had to use the calculator for every addition, subtraction and multiplication operation they did. As I noticed this, I asked her not to use the calculator for a couple questions to see what would happen and she had no confidence in any answer she was giving me. It was like I took her life line away from her and she wasn't able to do math anymore.

I think a major issue facing students today is the fear of making a mistake. I asked her why she needs to use the calculator for everything she did and she responded "so I know I am right." Maybe its a little shocking to me since I have been out of education for a while but I do not remember coming across this lack of confidence in doing even the most basic math skills. I called my mom, who is a secondary school math teacher, and she said the last 3-5 years has been getting worse and worse with students being like that. It was definitely and eye opening experience and a little bit scary.

Students Imagine the Future of Ontario's Education System

This graphic, created by students, was shared with me at a recent Adolescent Literacy Professional Development session and I thought it was worth sharing here.  I think there are a couple of areas of particular interest for math educators.

1.)   Practical Application:  “Why do we have to learn this?”  I am sure many of us have heard this before and “because it’s in the curriculum” is not good enough.  For me, the graphic reinforces the necessity of sharing those real world connections and applications with our students in order to get those “Ahhh..I get it!” moments.

2.)   Technology:  As we have discussed in the 7/8 Math course, there are many web based tools available in math education.  This graphic confirms for educators, students desire for technology in their learning. I thought “More Games” was interesting as we are learning that math games are an important part of a comprehensive math program.  

Connecting Math to Student Interests

Do you ever have students asking you "Why do we have to do this?  We are never going to use any of this once we leave school!"  Well, I forever have students saying that to me and so I am always looking for more examples of math connections for students, based on their interests and to keep them engaged, and to encourage them to keep taking math!

Not long ago, I came across this site which provides a multitude of math connections to consider.  In Math Central, under the tab Math Beyond School Grades 10-12, http://mathcentral.uregina.ca/beyond/browse/10-12 you will find (in alphabetical order) connections for math based on tonnes of different interests.  So, if you have a good class profile, you can see that one of your students is interested in earthquakes for example, to find the epicentre in an earthquake.  http://mathcentral.uregina.ca/beyond/articles/earthquakes/earthquakes.html

Earthquake Epicentre

Cool, right? And, there is a link to an interactive website where YOU can try to find the epicentre of an earthquake. http://www.sciencecourseware.org/VirtualEarthquake/VQuakeExecute.html

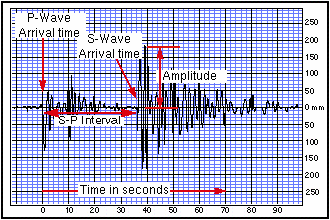What's a Seismogram?

The more we can show students examples of how math IS actually used in the real world and appeal to many different interests the more successful our students will be.

Money for Math Training

So I was looking through the internet for something a short while back, and came across this article: "Math training will open for all Ontario teachers"  It discusses the poor results on standardized tests for math students across the province, etc., etc.  Nothing we haven't heard before.  I did find a few things interesting that were stated in the article.

The first is, the article states that many elementary teachers are liberal arts grads, many of whom probably haven't taken a Math course since their last required one in high school.  I do recall in my professional teaching year, the P/J teachers had to do a Math proficiency test of some kind (I didn't have to take it myself, being I/S), and many of them were very anxious and nervous.  What did they learn in the program about teaching Math to kids?  If they had been prepared by the program, should they have been nervous?

The second interesting point, and I had read it in another article, was the teacher program is expanding from a 1 year to a 2 year program.  This would provide additional Math training for those elementary teachers who may be hesitant about teaching a subject they may not have liked in school.  This is wonderful!  Anything to ease the hesitation and doubt in a person's mind about teaching something is beneficial.  Also, the longer someone can spend practicing, and doing something, the more they will understand and feel comfortable about it.  Of the previous 10 weeks of placement, how much of that was spent teaching Math to elementary school kids?  The first week was supposed to be "observation"...so that leaves 8 weeks...8 weeks for a new person to get their bearings, and develop a routine, become familiar with the students, etc.  To become an electrician , a person has to put in 9000 hours of apprenticeship work.  That is usually after a pre-apprenticeship program.  9000 hours!  Who ever thought teachers only need 8 weeks?

Lastly, the article mentions high school Math teachers are specialists.  Now they must be using this as a relative term, because I don't know very many people with a Math specialist.  Up until the last couple of years, you didn't even need to be qualified to teach up to grade 10 Mathematics; my school board has now been enforcing qualifications when possible.  I see the addition of Intermediate Math qualifications as a move in the right way.

At the end of the day, better training for teachers can't hurt students.  But will EQAO scores change?  We will have to wait at least 2 years to find out!

First World Problems?!

I came across another article I thought was a great integration of "real" world connections to math. Often in my classroom I hear my students tell me "this is pointless" or ask "how is this even useful?" These comments and questions are most often heard during my math lessons!! I try to explain to them that math is everywhere. Although this article doesn't mention numbers. It does say he is a billionaire! This article was taken and broken down into a problem solving framework, and can also link other curriculum content. I think they did a fantastic job in creating a lesson connecting this very brief article.


http://emergentmath.com/2014/05/09/larry-ellison-billionaire-ceo-makes-unsound-business-decisions-with-regards-to-his-basketball-playing-on-his-yacht/

Making Math Fun!

I came across this link when I was looking at the different blogs and had to share. It's a great resource for a variety of math review games. With EQAO and unit tests, these games give students an opportunity to make math fun and more memorable. They are simple games that can be applied to several grades and across all strands.
I remember when I was teaching science to Grade 9's they always got really excited about playing games to review. Math is no different! It's intimidating for a lot of students sometimes and overwhelming to try to remember so many methods, rules and formulas when they sometimes don't even have the foundational math skills. Any opportunity to ensure students can remember and apply the math skills they are learning in a fun and interactive manner will likely increase the chances of them being able to apply the skills.


http://croitz.blogspot.ca/2012/07/made-4-math-3-feeling-lucky.html

Inflation?!

Macleans recently published an article about OSIE dropping seats in their B.Ed program and adding 500 to their Masters program. I'm not here to discuss if this is a good idea or not, rather use the information given as a teachable moment. Taking the numbers provided, we can use this as a way help students make real-world connections and they can determine who really benefits from this decision!

http://www.macleans.ca/education/post-graduate/anger-as-u-of-t-drops-bachelor-of-education/

Satan's Handiwork?

Perhaps declaring the Common Core approach as "Satan's Handiwork", as one parent did, was a little overboard, but lets take a look at what all the fuss is about.  I had heard a little about the Common Core curriculum that was spreading in the U.S., the attached article provides a little insight into how it is being received by the public.  ABC News article  The Common Core approach aims to change the way students look at math by incorporating more conceptual understanding to go along with the procedural knowledge.  The problem, as outlined by parents and critics, is that the concepts are beyond what the students are capable of and differ vastly from the traditional math that the parents know and understanding, creating a void in understanding during homework.  Here are some sample Common Core problems.  What do you think?
Here are some of the questions: 61-38=, 21-6=, 123-59=...

.

Smart Exchange

 

I was introduced to Smart technology about 4 years ago at a school PD session lead by the math department head.  Like much PD it was a great resource and tool, but to find the time to incorporate into my courses was the challenge.  And the information provided was focused on the capabilities for math, which I was not teaching at the time.  We had a few Smart Boards throughout the school but most teachers were using it as a projection screen and not utilizing all the potential it has.  I have to admit, I was doing the same.  I had recently converted most of my course content to PowerPoint and did not understand the different between Notebook and Power Point.  Fortunately, I have the opportunity to attend a 2 day PD session the summer to really understand the use of Smart in the classroom.  This time allowed me to become comfortable with the technology and try to incorporate Smart into my classes.  I was also introduced to Smart Exchange at this PD session which provided an abundant of resources and ideas to help generate lessons.  The Gallery Essential and Lesson Toolkit provide subject specific templates created in flash for you to use and adapt in your course.  Smart Notebook is now my first choice when creating teacher-directed lessons.  I also encourage my students to create presentations and use some of the available tools I use in lessons for their assignments.  Its a very user friendly and interactive program that continues to improve student engagement.  And the Smart Exchange website provides even more teacher created resources to share by subject and grade.  Sometimes you don't have to reinvent the wheel, you just have to tweak it!  

Well, yesterday I had my first real introduction to Khan Academy.  I have to say, I really like it.  If you are like me, someone who didn't have trouble with math, but needed some review and tutorials to remember what has long been lost, then Khan could be a great tool.  I really enjoyed how I could visually see the scaffolding of learning, how one topic fed into another.  It was hugely beneficial to receive hints and answers to questions you were struggling on.  I also found that the method of teaching is something that I could definitely benefit from, though I know there are detractors.  Here is an example from Khan Academy of how the topics are represented as part of a web of learning.

While perusing the net for math related news I came across a Washington Post article on Danica McKellar (of Wonder Years fame.)  Since her spell in hollywood, Danica has become a vocal advocate for math with her books Math Doesn't Suck and Kiss My Math.  McKellar is more than just a celebrity looking to cash in however, as she studied mathematics at UCLA, graduating summa cum laude in 1998.  What a wonderful role model for our young ladies today.  She has a math blog of her own that is found on her website.

 

Flipped classroom

Why I flipped my classroom

I love this teaching model because allows teachers to spend more one on one time with each student. This requires the students to watch at home teacher created videos.
Some of the benefits of Flipped Classroom are:

• students can choose their own pace to go through the materials provided.
• they get involve through activity in classroom instead of listening to a long  lesson presented by the teacher.
• frees up the lecturers time so more one on one time can be spent with students that needs help.

Some of the drawbacks of the Flipped Classroom are:

• all the students need to have access to a computer and to Internet.
• they have to be motivated to go through material provided at home.

Why I Flipped my Classroom

And another interesting video to watch : The basics of blended learning

Math is Fun

I was recently surfing the web (does anyone still say that?) when I came across this website called Math is Fun (Mathsisfun.com). The website begins with a picture of various topics in math such as algebra and geometry and also with resources such as worksheets and games. 

Upon clicking a topic, you are sent to a page with a breakdown of sub topics within it. These are very informative and have full lessons for a student to go through along with many examples. Further down on the first page is also a teacher page which leads to fun activities for your classroom and even quizzes for your students.

I think this is a great resource to have to get the students out of the classroom and also to potentially use for a flipped class lesson. A teacher can direct their students to the appropriate link for them to look over and take notes from as homework and then provide worksheets the following day in class to practice problems and to ensure student understanding.

It is a resource that can help make math fun!

The Future of Math

There has been considerable concern over education in Ontario in recent years, with a particular emphasis on students struggling with mathematics.  I can remember doing provincial testing as a student in grade 9, and teachers congratulating us on our scores, which compared favourably to the rest of the province that year (thank you Mrs. Belanger and Ms. Thornton).  I also remember teachers telling us how lucky we were because our education system was widely regarded as one of the best. At that time I wasn't all that concerned with student math scores across the province, or any score for that matter, so I'm not sure if what they were saying was true.

Now a teacher, what I do know is that one of the subjects parents care a great deal about is math.  I've been at parent teacher interviews having taught geography, phys-ed, and history at the secondary level, and very seldom does a parent bother to drop in. I've also been at parent teacher interviews in for a grade 8 class. After the generic question "How is my child doing?", often parents want to know about math and english. The same is true at the secondary level, as everyone can see by the long line of parents waiting to see the math and english teachers.

I also know that a lot of times parents are concerned about math because their kids struggle with it.  In this article, Martin Regg Kohn documents Ontario's math scores, which have fallen from 11th place in the PISA (Program for International Student Assessment) rankings in 2003, to 19th place in 2012. To make matters worse, EQAO scores for grade 6 students meeting the provincial standard saw a drop from 62% to 56% in 2009. So it doesn't look like the recent trend is going to change in the immediate future.  Although not everyone agrees that these scores are accurate predictors for future success, you have to think that parental concerns, and the ensuing political pressure that comes with it, will lead to changes in curricula, teaching methods, and professional development.

School boards wouldn't be offering extensive professional development sessions, invest significantly in technology in the classroom (macbooks, smartboard, graphing calculators), or be obsessing over EQAO scores (and the funding associated with it) if these scores didn't matter or students weren't struggling.  The province also wouldn't have launched a $4 million dollar incentive budget to encourage existing teachers with degrees in humanities to take math courses, presumably to increase the level of math literacy in its schools.

What I don't know and can't predict is what changes are going to be made. But I know they're coming.

Math Specialists

I found this article interesting because it's actually the reason why I chose to enroll in the ABQ math intermediate math course.  The results from the most recent provincial math tests showed that only 57 percent of grade 6 students were meeting expectations, and only two-thirds of grade 3 students were processing math at the levels they should be.  Naturally this puts a lot of pressure on schools and teachers to improve math education in the classroom.

The government has decided to try and remedy this situation by encouraging teachers to upgrade their qualifications to become math specialists.  They have done this by offer partial subsidies to teachers who enroll in math-related AQ courses, and making it easier for teachers to qualify to take these courses.

I think this is a great idea.  I can't think of a downside towards urging teachers to become more proficient at the subjects they teach, especially if it's a subject that they didn't study in university.  At the very least, it's a good idea for teachers to familiarize themselves with alternative teaching strategies and different ways of reaching students.

In addition to the above strategies, I think schools should also make an effort to rotate teachers within a school so that teachers are teaching their specialty wherever possible.  While this would require some significant planning and organization, it just makes sense to me.  I have personally been put in a position during my teaching career where I was not only expected to teach a subject that I didn't study in university, but also one that I didn't study in high school (grade 12 physics).  As hard as I tried, there is no way I could match the expertise of someone who is fully qualified to teach the subject.

Unfortunately this article gets a little bit too political for my tastes by the end.  I understand that certain parties may have mixed motives, but I would like to see the focus begin and end with student success.

Overall, I applaud the effort.  It's great that they were able to identify a problem through standardized testing, and it's great that the government is making an effort to remedy the situation.

http://www.cbc.ca/news/canada/toronto/ontario-wants-to-see-more-math-specialists-in-classrooms-1.2489046

Parents, educators rally against Alberta's "New Math"

I came across this news article, originally published this past April, that tells the story of over 200 parents who protested in response to changes in Alberta's math curriculum.

The new math curriculum focuses on "discovery-based" learning in the classroom.  The parents argued that students are already having difficulty demonstrating core math skills, and that removing even more focus on developing these skills is a bad idea.

There were a few things about this story that struck me as interesting.  For starters, it is great to see a large group of parents that are so passionate about education.  There was a large public gathering where people made signs and marched, as well as a petition that currently has over 13,000 signatures.

(Picture taken directly from the news article)

This story is also an example of the need for transparency between the schools and the parents.  One of the signs in the picture read "Where's the proof?".  In my opinion, in order to justify making such a significant change to the math curriculum, sufficient research should be gathered, interpreted, and made available.  This research should focus on proving that students are somehow better off focusing less on fundamental math skills and more on application questions.  From the information presented in this article alone, it's clear that either an insufficient amount of research was conducted, or the findings have not been passed on to concerned parents.

Personally, I've noticed in Ontario schools that basic math skills are lacking.  I would love to see changes to the curriculum that renews focus on developing important math skills that students will need throughout their education.

http://www.cbc.ca/news/canada/edmonton/parents-educators-rally-against-alberta-s-new-math-1.2608360

New Vs. Old Fashioned

Here is a picture that I saw the other day. Many of you may have seen this already as it appears to be circulating on various social media websites.

At first glance, I was thinking this is ridiculous. What in the world is this? Are we supposed to teach math like this? What do all these numbers really mean? It appears to be a method of doing subtraction that takes multiple steps of addition that seem to make no sense at all. I read this article on the topic and it made much more sense to me. 

The upper portion is how many of us learned to do subtraction questions. Often times, these numbers that we determine are based on what the calculator tells you, what you calculate with your fingers, or what you have memorized over the years.

The bottom portion is something many of us actually do in our heads. When I look at the question 32 - 12, yes I know the answer is 20 (from memorization) but if I needed to calculate it in my head, I would think 12 to 22 is 10, 22 to 32 is also 10. So now, 10 and 10 make 20. This is also how many of us calculate how much change we should get back when we pay for an item or service. We calculate how many cents to get to the next dollar, and then just add up how many more dollars we need.

Example:

You owe $4.90, and you hand the cashier a $20.

$20 – $4.90

To perform the mental math, I would think $0.10 to get to $5, and then $15 to get to $20. Thus, I would get $15.10 in change back.

Essentially, that is what the bottom half of the original picture is depicting. The article also had a second image, which contains an easier description of how this method works.

I think this is a great way to teach subtraction, but I do not think it should be the only method that is used. Students need to be given the option of which method suits their understanding the most and be allowed to use it accordingly. 

Ted and Algorithms

http://www.ted.com/talks/kevin_slavin_how_algorithms_shape_our_world

How algorithms shape our world.

This is a video from TED Global, Kevin Slavin argues that we're living in a world designed for — and increasingly controlled by — algorithms. This video shows a riveting talk from TED Global, he explains how more complicated computer programs calculate: espionage tactics, stock prices, movie scripts, economics, insurance rates and architecture. He explains that this is a dangerous line to be in between, the algorithm codes that are being written are going to give us codes that we don’t truly understand. This will give us implications we would not be able to control.

It’s an interesting concept that Kevin Slavin states, however the evidence that are presented do have merits to take into consideration. It is a video that should be watched and taken into consideration.

Math Games

http://www.coolmath.com/algebra/

This website is a great way for students to interact by going to http://www.coolmath.com. The website has numerous ways for students to learn algebra by reviewing videos to going on to games that allow them to have an entertaining experience at the same time learn.

Considering that youths today have grown with technology from birth, there is evidence that they have become obsessed with devices. Going on-line, playing video games, is the norm; coolmath.com is capable to give these students that interaction stimulation that can be learned by playing video games and watching videos. These skills and techniques that students can learn on coolmath.com would give them learning life skills, and math strategies. Critical thinking is achieved by practicing through repetition by have a fun interaction through websites such as coolmath.com student will achieve life survival skills that are needed today in society

Rice Paddies and Math Tests

I am not sure if anyone has read any of Malcolm Gladwell’s books but I am a huge fan and highly recommend them. In particular, I want to quickly take a look at the book Gladwell wrote called Outliers. This book looks at the story of success and what makes high achievers different from others.  Gladwell argues that we must focus on contributing elements around ones family, culture, generation, experience and upbringing.

The short story that I invite you to take a look at this short storty called, Rice Paddies and Math Tests. http://gladwell.com/outliers/rice-paddies-and-math-tests/

The significance of mathematics:

Certain Asian cultures have an early head-start in math compared to their Western counterparts, but it is not due to studying at an earlier age. It is based in the fundamentals of their language. The linguistics of our numerical system is organized in a very clumsy manner, and its structure doesn’t make a lot of sense. The following passage from this chapter could not have been stated any better:

In English, we say fourteen, sixteen, seventeen, eighteen, and nineteen, so one might expect that we would also say oneteen, twoteen, threeteen, and fiveteen. But we don’t. We use a different form: eleven, twelve, thirteen, and fifteen. Similarly, we have forty, and sixty, which sound like the words they are related to (four and six). But we also say fifty and thirty and twenty, which sort of sound like five and three and two, but not really. And, for that matter, for numbers above twenty, we put the “decade” first and the unit number second (twenty-one, twenty-two), whereas for the teens, we do it the other way around (fourteen, seventeen, eighteen). The number system in English is highly irregular. Not so in China, Japan, and Korea. They have a logical counting system. Eleven is ten-one. Twenty is ten-two. Twenty-four is two-tens-four and so on.

(The above paragraphs was retrived from the following website, http://fosterreisz.wordpress.com/2010/03/25/outliers-the-story-of-success-–-rice-paddies-and-math-tests/ )

What are your thoughts on this?